Indice
I componenti e le reti a regime sinusoidale
Concetti fondamentali:
- sinusoide (vedi anche paragrafo della sezione 1C e appunti di quarta (ripasso terza)
- da matematica:
- funzioni trigonometriche seno, coseno, tangente, arcotangente
- numeri complessi e operazioni con i numeri complessi, significato della moltiplicazione per j (rotazione 90°)
- operazioni con i vettori (graficamente addizione e sottrazione, analiticamente per prodotto rapporto)
Il regime sinusoidale
Nei circuiti in alternata tensioni e correnti sono sinusoidi con la stessa frequenza. Per studiare questi circuiti è necessario:
- conoscere le sinusoidi
- applicare il metodo simbolico
- conoscere il concetto di impedenza
In particolare, sostituendo ai componenti passivi delle impedenze e svolgendo i calcoli con il metodo simbolico è possibile utilizzare tutte le leggi e i metodi validi per la continua.
Sinusoide
Una tensione sinusoidale cambia nel tempo con la legge:
`v(t)=V_max sen(omega t + varphi)`
Dove:
- Vmax è il valore massimo, legato al valore efficace (valore equivalente in continua) dalla formula `V = V_max/sqrt(2)`
- ω è la pulsazione, legata alla frequenza f dalla relazione `omega=2 pi f`
- φ è la fase, legata al ritardo o anticipo rispetto alla sinusoide che passa per l'origine dalla relazione `t_text(r/a)= varphi/omega`
Vedi anche paragrafo della sezione 1C.
Metodo simbolico
Lo studio dei circuiti in alternata è agevolato se si rappresenta ogni corrente e ogni tensione con un vettore di ampiezza pari al valore efficace e angolo pari alla fase (la frequenza non è interessante perché uguale per tutte le grandezze). A sua volta i vettori possono essere rappresentati con dei numeri complessi:
`v(t)= sqrt(2)V sen(omega t + varphi) to bar V = V _varphi = V cos varphi + j V sen varphi`
La trasformazione delle sinusoidi in vettori o numeri complessi - grandezze costanti caratterizzate da due soli valori - facilita molto i calcoli. Alla fine del procedimento si esegue una anti-trasformazione per ritornare alle sinusoidi:
`bar V = a+jb to {(V = sqrt (a^2+b^2)),(varphi=text(arctg) b/a +- 180°):} to bar V = V _varphi to v(t)= sqrt(2)V sen(omega t + varphi)`
Componenti passivi in regime sinusoidale
Consideriamo la tensione ai capi del componente e la corrente che scorre sul componente e ricaviamo la relazione tra queste due grandezze dalle rispettive leggi di Ohm. L'espressione di v e i come sinusoidi1) è:
`v=sqrt(2)Vsen(omegat + varphi_v)`
`i=sqrt(2)Isen(omegat + varphi_i)`
In regime sinusoidale la pulsazione (quindi la frequenza e il periodo) è uguale per tutte le grandezze, quindi si tratta di trovare il legame tra i rispettivi valori efficaci e tra le fasi. Definiamo anche la grandezza sfasamento come l'angolo tra la fase della tensione e quello della corrente. Analiticamente:
`varphi = varphi_v - varphi_i`
Questo indica il ritardo che c'è tra tensione e corrente:
- uno sfasamento positivo indica che la tensione è in anticipo
- uno sfasamento negativo che la tensione è in ritardo (la corrente in anticipo)
- uno sfasamento pari a zero indica che le due grandezze sono in fase (hanno la stessa fase)
Ricaveremo le relazioni tra tensione e corrente considerando le rispettive sinusoidi poi vedremo che le stesse relazioni possono essere espresse in maniera molto più semplice utilizzando il metodo simbolico.
Resistore
Vale la legge di Ohm
`v=Ri`
La relazione è lineare attraverso il parametro R. Se sostituiamo le sinusoidi nella legge di Ohm otteniamo:
`v=Ri=Rsqrt(2)Isen(omegat + varphi_i)`
mettendo in evidenza la relazione tra i valori efficaci e tra le fasi:
`{(V=RI), (varphi_v=varphi_i):}`
Quindi le due grandezze sono in fase (sfasamento zero) e la relazione tra i valori efficaci corrisponde a quella che vale nei circuiti in continua. Possiamo esprimere queste due relazioni con una sola espressione usando il metodo simbolico scrivendo:
`bar V = R bar I`
dove compaiono i vettori (o numeri complessi) che rappresentano le due sinusoidi. Questa relazione, oltre ad essere una sola, è più semplice e riguarda grandezze costanti. La figura 8 del testo mostra un diagramma vettoriale con le due grandezze (allineate perché lo sfasamento è zero) e un grafico con le due sinusoidi2).
Condensatore
Procediamo come per il resistore. Sostituendo le sinusoidi nella legge di Ohm otteniamo3):
`i = C (dv)/(dt)= omega C sqrt(2)Vsen(omegat + varphi_v + 90°)`
mettendo in evidenza la relazione tra i valori efficaci e tra le fasi:
`{(V= 1/(omega C) I), (varphi_v=varphi_i - 90°):}`
Quindi la tensione è in ritardo di 90° (sfasamento -90°) rispetto alla corrente e la relazione tra i valori efficaci dipende dalla capacità C ma anche dalla pulsazione (si veda questo grafico interattivo per osservare le due sinusoidi). Questa caratteristica del condensatore è particolarmente importante e viene sfruttata in tante applicazioni: il comportamento del condensatore dipende dalla frequenza! Possiamo esprimere queste due relazioni con una sola espressione usando il metodo simbolico scrivendo:
`bar V = -j 1/(omega C) bar I`
dove -j indica una rotazione di 90° in senso orario (negativo) che aggiunge un ritardo alla tensione rispetto alla corrente.
Se definiamo reattanza capacitiva4) la grandezza:
`bar (X_C)=-j1/(omega C)= {:X_C:}_(-90°) [Omega]`
possiamo riscrivere la legge di Ohm per il condensatore quando si usa il metodo simbolico così:
`bar V = bar(X_C) bar I`
che somiglia a quella della resistenza ma con la reattanza capacitiva al posto della resistenza5). La figura 9 del testo mostra un diagramma vettoriale con le due grandezze sfasate di -90° (corrente in anticipo) e un grafico con le due sinusoidi.
Induttore
Sostituendo le sinusoidi nella legge di Ohm dell'induttore otteniamo:
`v = L (di)/(dt)= omega L sqrt(2)Isen(omegat + varphi_i + 90°)`
mettendo in evidenza la relazione tra i valori efficaci e tra le fasi:
`{(V= omega L I), (varphi_v=varphi_i + 90°):}`
Quindi la tensione è in anticipo di 90° rispetto alla corrente (sfasamento 90°) e come per il condensatore la relazione tra i valori efficaci non dipende solo dall'induttanza L ma anche dalla pulsazione (si veda questo grafico interattivo con le due sinusoidi). Anche in questo caso si potrà sfruttare il fatto che il comportamento dell'induttanza dipende dalla frequenza. Possiamo esprimere le due relazioni viste sopra con una sola espressione usando il metodo simbolico scrivendo:
`bar V = j omega L bar I`
dove j indica una rotazione di 90° in senso antiorario che giustifica l'anticipo della tensione rispetto alla corrente.
Se definiamo reattanza induttiva la grandezza:
`bar (X_L)=j omega L= {:X_L:}_(90°) [Omega]`
possiamo riscrivere la legge di Ohm per l'induttanza quando si usa il metodo simbolico così:
`bar V = bar(X_L) bar I`
che somiglia a quella di resistenza e capacità ma con la reattanza induttiva (in Ohm). La figura 10 del testo mostra un diagramma vettoriale con le due grandezze sfasate di 90° (tensione in anticipo) e un grafico con le due sinusoidi.
Impedenza
E' possibile accorpare i tre componenti passivi R, L e C in un unico termine detto impedenza, così definito:
`bar Z=R+j(omega L - 1/(omega C))=R+jX=Z_varphi [Omega]`
dove Z è l'impedenza, misurata in Ohm, espressa come numero complesso o come vettore. Il termine X è la reattanza totale somma della reattanza induttiva:
`bar X_L =j omega L = jX_L= {:X_L:}_(90°)[Omega]`
e di quella capacitiva:
`bar X_C =-j 1/(omega C) = -jX_C= {:X_C:}_(-90°)[Omega]`
Al posto di tre componenti e tre leggi di Ohm si utilizzerà un unico componente, l'impedenza, e una sola legge di Ohm:
`bar V= bar Z cdot bar I`
Si osserva che:
- l'angolo φ è compreso tra -90° e 90° e coincide con lo sfasamento tra tensione e corrente
- condensatori e induttori si comportano diversamente alle varie frequenze perché le rispettive reattanze dipendono da ω
Analisi di circuiti in regime sinusoidale
Le leggi e i principi utilizzati per i circuiti in continua (serie-parallelo, principi di Kirchhoff, sovrapposizione degli effetti, ecc.) valgono anche in regime sinusoidale ma per utilizzare gli stessi procedimenti bisogna prima:
- trasformare tensioni e correnti sinusoidali in vettori o numeri complessi con il metodo simbolico
- calcolare le impedenze dei vari rami da utilizzare al posto di resistenze, capacità e induttanze
A quel punto si può procedere applicando regole e metodi dei circuiti in continua tenendo presente però che il calcolo sarà più laborioso perché tutte le grandezze saranno vettori/numeri complessi e che al posto della resistenza comparirà l'impedenza. L'ultima fase del problema sarà sempre una trasformazione inversa per esprimere tensioni e correnti come sinusoidi a partire dai vettori corrispondenti.
Esempio: analisi di un circuito in AC
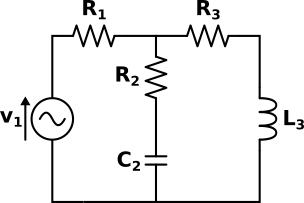
Dato il seguente circuito:
dove la tensione del generatore6) vale `v_1 = sqrt(2)12sen(314t - 30°)` e i componenti hanno i seguenti valori: R1 = 1,8 kΩ, R2 = 3,3 kΩ, R3 = 2,2 kΩ, C2 = 330 nF e L3 = 6,8 H. Calcolare le correnti nei tre rami.
Trasformiamo la tensione in vettore/numero complesso per utilizzare il metodo simbolico7):
`bar V_1 = 12_(-30°)=10,4-j6 V`
Calcoliamo le impedenze dei tre rami:
`bar Z_1 = R_1 = 1,8kOmega`
`bar Z_2 = R_2 -j1/(omega C_2)=3,3 -j1/(314 cdot 330 cdot 10^(-6))=3,3-j9.6 kOmega`
`bar Z_3 = R_3 +j omega L_3=2,2 +j314 cdot 6.8=2,2+j2,1 kOmega`
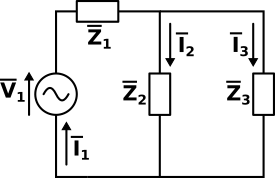
Il circuito può essere ridisegnato così:
A questo punto si procede come per i circuiti in continua: dal momento che è presente un solo generatore si userà il metodo della resistenza (impedenza in questo caso!) equivalente per calcolare la corrente nel ramo del generatore, poi si risalirà alle altre due correnti.
Calcoliamo l'impedenza equivalente di `bar Z_2` e `bar Z_3` in parallelo8):
`bar Z_(23)= (bar Z_2 bar Z_3)/ (bar Z_2 + bar Z_3)=[(3,3-j9,6)(2,2+j2,1)]/(3,3-j9,6 + 2,2+j2,1)=3+j1,5 kOmega`
Dopo aver ridisegnato il circuito (non lo farò in questo esempio) calcoliamo l'impedenza equivalente:
`bar Z_(eq)=bar Z_1 + bar Z_(23)=1,8+3+j1,5=4,8+j1,5 kOmega`
Applicando la legge di Ohm si può calcolare la corrente che circola sul ramo del generatore:
`bar I_1 = bar V_1 / bar Z_(eq)= (10,4-j6)/[(4,8+j1,5)cdot 10^3]=1.6-j1.7=2.4_(-47°) mA`
Le altre correnti si possono trovare con procedimenti diversi. Scegliamo di usare la sola legge di Ohm calcolando prima la tensione ai capi di Z23:
`bar V_(Z_23) = bar Z_(23) bar I_1=(3+j1,5)cdot 10^3 (1.6-j1.7) cdot 10^(-3)=7.4-j2.7 V`
Allora le ultime due correnti si trovano con:
`bar I_2=bar V_(Z_23)/bar Z_2= (7.4+j2.7)/[(3,3-j9.6)cdot10^3]=0.5+j0.6=0.8_(51°) mA`
`bar I_3=bar V_(Z_23)/bar Z_3= (7.4+j2.7)/[(2,2+j2,1)cdot10^3]=2.4-j1=2.6_(-24°) mA`
Applicando la trasformazione inversa del metodo simbolico risaliamo alle tre sinusoidi delle correnti:
`i_1 = sqrt(2) cdot 2,4 sen (314t -47°)`
`i_2 = sqrt(2) cdot 0.8 sen (314t +51°)`
`i_3 = sqrt(2) cdot 2,6 sen (314t -24°)`