Il capitolo tratta dettagliatamente il problema delle misure elettriche e definisce le caratteristiche dei segnali. Qui faremo solo brevi cenni agli argomenti più importanti che per motivi di tempo non possono essere trattati nel corso. La parte sulle misure fa parte del programma del biennio (fisica, chimica, scienze e tecnologie applicate).

Caratteristiche di un oggetto/fenomeno quantificate con una grandezza.

Misura ottenuta dal confronto con un termine di paragone stabilito convenzionalmente, l'unità di misura.

Sistema internazionale: convenzione che stabilisce quale UDM utilizzare per ogni grandezza (vantaggi: uniformità, evitare conversioni, UDM corretta quando si applicano le formule).

Ogni misura è affetta da errori (strumento, ambiente, metodo, operatore, ecc.). La misura perfetta non esiste.

Errori:

• sistematici: si ripetono sempre allo stesso modo (possono essere valutati e compensati)
• accidentali: casuali (stimabili statisticamente)

Il valore vero di una misura non è mai noto ma dato l'errore assoluto è definito un intervallo di incertezza (valore misurato ± errore assoluto) che comprende il valore vero. Più piccolo è l'errore assoluto e più piccolo è l'intervallo quindi più precisa è la misura.

L'errore relativo (percentuale), definito come rapporto tra errore assoluto e valore misurato (moltiplicato per 100), permette di confrontare più misure e stabilire quale è più precisa.

Vedi il_multimetro

Vedi il_multimetro

Vedi alimentatore_stabilizzato

Segnale come grandezza che rappresenta un'informazione.

Definizioni:

• segnale periodico: si ripete nel tempo
• periodo `T [s]`: ogni quanto si ripete
• frequenza `f=1/T [Hz]`: quante volte al secondo si ripete (in Hertz)

Unipolare o unidirezionale: sempre maggiore o uguale (o sempre minore o uguale) a zero.

Il valore medio coincide con la componente continua di un segnale. Osservando la figura 10 si definisce valore medio la differenza tra l'area compresa tra il segnale e l'asse del tempo quando il segnale è positivo e quando è negativo e il periodo del segnale: `V_m= (A_+ - A_-)/T`

Un segnale è alternato se ha valore medio nullo (non ha componente continua).

Il valore efficace (RMS in inglese) di un segnale è quel valore che in continua produce gli stessi effetti per quel che riguarda la potenza¹⁾.

Negli impianti in alternata (vedi Tecnologia e Progettazione) l'ampiezza di tensioni e correnti è sempre espressa indicando il valore efficace.

In figura 12 il segnale sinusoidale (o armonico) o sinusoide. E' il segnale più importante ed è descritto dalla formula:

`v(t)=V_(MAX)sen(omega t + varphi_v)`

dove:

• v(t) indica la tensione che cambia un funzione del tempo (spesso scriveremo solo v perché il carattere minuscolo implica la dipendenza dal tempo)
• V_MAX è il valore massimo della tensione (anche detto valore di picco V_P)
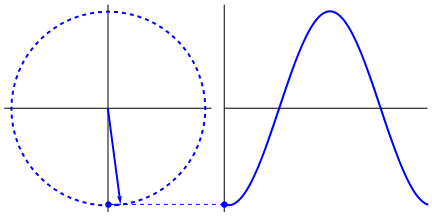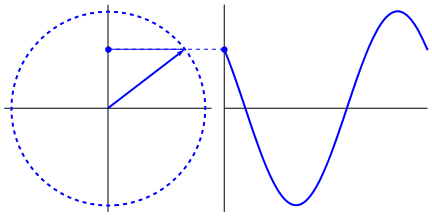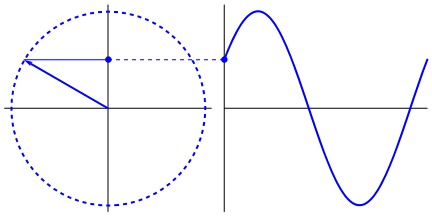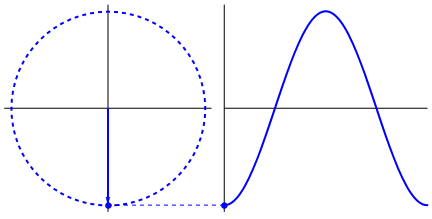
• sen è il seno, una funzione trigonometrica che si applica agli angoli che coincide con la proiezione sull'asse y del segmento che individua l'angolo in un cerchio trigonometrico (di raggio unitario) (vedi seno)
• ω è la pulsazione, una velocità angolare espressa in [rad/s], costante per una sinusoide, legata ai valori di frequenza e periodo dalla relazione `omega = 2 pi f=(2 pi) /T`²⁾
• ωt è un angolo che cambia nel tempo con velocità costante
• φ_v è la fase della tensione; è un angolo costante che si somma a ωt e che indica il ritardo o l'anticipo della sinusoide rispetto ad un'altra uguale ma che passa per l'origine (il tempo di ritardo o di anticipo si calcola con `t_(RA) = varphi_v/omega`)

Una sinusoide è una funzione del tempo il cui valore corrisponde al seno³⁾ di un angolo che cambia nel tempo con una velocità costante pari alla pulsazione (vedi questa animazione di Wikipedia).

Un segnale sinusoidale è dunque descritto da tre parametri (vedi questo grafico interattivo):

• ampiezza V_MAX
• pulsazione ω
• fase φ_v

Per descrivere l'ampiezza della sinusoide, in alternativa al valore massimo, si può usare il valore efficace - per le sinusoidi vale `V_(eff)=V_P/sqrt(2)` - o il valore picco-picco `V_{PP} = 2 V_P`. Al posto della pulsazione invece si possono indicare il periodo T (visibile nel grafico o nel display di un oscilloscopio) - o la frequenza f (misurata dagli oscilloscopi e impostata nei generatori di funzione); le tre grandezze indicano in maniera diversa la stessa proprietà.

Il testo riporta grafico e caratteristiche principali di molti altri segnali tipici:

• segnale sinusoidale raddrizzato (solo onda positiva) a singola semionda e doppia semionda
• segnale triangolare (alternato e unidirezionale)
• segnale a dente di sega
• segnale a onda quadra (alternta e unidirezionale)
• segnale a onda impulsiva (rettangolare)

Per l'ultimo segnale, particolarmente importante nell'elettronica digitale, si definisce duty-cycle il rapporto tra il tempo in cui il livello del segnale è alto e il periodo:

`D=t_d/T`

Questa grandezza sarà particolarmente importante in tante applicazioni e verrà spesso indicata in forma percentuale:

`D_%=t_d/T * 100`

Si calcola con la formula:

`V_(eff) = sqrt(V_m^2+V_(eff\ ac)^2)`

dove compaiono il valore medio (componente continua) e l valore efficace della sola componente alternata.

Vedi il_multimetro

Il generatore di funzione genera segnali in tensione con forma d'onda e caratteristiche regolabili. L'uscita del generatore è un Connettore_BNC - a baionetta - dove collegare un cavo coassiale (figura 25b). Il segnale viaggia nell'anima del cavo (conduttore centrale), protetto da un isolante (dielettrico), mentre la calza schermante serve sia come schermo elettrico, per proteggere il segnale da disturbi esterni, che come riferimento a massa. Il segnale generato può essere “sdoppiato” utilizzando un connettore T (tee), ad esempio per visualizzare il segnale all'oscilloscopio e contemporaneamente applicarlo in un circuito.

Le principali regolazioni disponibili su un GdF sono:

• forma d'onda: sinusoidale, triangolare e rettangolare
• frequenza (impostabile selezionando il range di frequenza e ruotando una manopola)
• ampiezza del segnale (valore picco-picco o valore di picco della tensione)
• eventuale attenuazione del segnale (20dB produce un segnale 10 volte più piccolo)
• offset o componente continua del segnale
• simmetria del segnale (utilizzato in particolare per impostare il duty-cycle dell'onda rettangolare)

Spesso il GdF dispone di un'uscita TTL compatibile: il segnale presente in questo connettore BNC è sempre rettangolare con ampiezza e offset fissi (in genere si alternano 0 e 5 Volt) mentre frequenza e duty-cycle sono regolabili.

L'oscilloscopio digitale è un strumento che serve a visualizzare segnali in tensione su uno schermo. I segnali sono applicati agli ingressi (chiamati canali o tracce) con un connettore BNC. Il connettore permette un facile collegamento con un generatore di funzione dotato di uscita BNC o con un circuito, usando un cavo BNC che termina con una sonda o con due morsetti a coccodrillo o semplicemente con due fili da inserire in una breadboad.

Lo schermo dell'oscilloscopio presenta una griglia con 10 divisioni in larghezza e 8 in altezza (l'origine al centro). Nello schermo i segnali sono rappresentati secondo due modalità:

• in modalità x-y (usata raramente) due ingressi sono usati per le due coordinate
• in modalità con base dei tempi interna i segnali applicati agli ingressi sono usati per la coordinata y mentre il tempo, regolato internamente, è usato per l'asse x

In entrambe le modalità di funzionamento l'oscilloscopio ridisegna continuamente lo schermo lasciando una traccia secondo le coordinate dettate dai segnali (se il segnale cambia molto lentamente è possibile seguire questa traccia che “percorre” lo schermo da sinistra a destra per poi ricominciare). Le varie schermate appaiono come un'unica immagine ferma se lo strumento è “sincronizzato” col segnale; in questo caso si può studiare l'andamento nel tempo del segnale ed eventualmente fare delle misure.

Gli oscilloscopi sono strumenti piuttosto complicati e dotati di molte regolazioni; le principali sono:

• scelta della modalità (x-y o base dei tempi interna)
• impostazioni del trigger, il circuito che permette di sincronizzare (e quindi “fermare”) le schermate, in particolare:
  • canale/traccia usata per la sincronizzazione (ad esempio se è presente un solo segnale nell'ingresso 1 occorre impostare CH1)
  • livello del trigger, valore di tensione che corrisponderà alla coordinata y nell'origine, cioè al centro della griglia (ovviamente deve essere un valore assunto dal segnale selezionato come sorgente per il trigger)
• V/div per impostare la scala per l'asse y (quanti Volt per ogni divisione)
• t/div per impostare la scala per l'asse x (quanti secondi per ogni divisione)
• manopola position, per traslare il segnale in alto o in basso
• manopola x-position, per traslare il segnale a destra o sinistra
• impostazioni per le singole tracce:
  • accoppiamento:
    • DC per osservare il segnale così com'è
    • AC per eliminare la componente continua del segnale e osservare solo quella alternata
    • GND per vedere un retta orizzontale corrispondente a 0 Volt
  • attenuazione (deve essere x1, a meno che non si usi una sonda)
  • inversione, per invertire il segnale

Esistono tantissime altre funzioni:

• un tasto auto-set che imposta automaticamente l'oscilloscopio
• un tasto measure per misurare le varie caratteristiche del segnale
• un tasto cursor per visualizzare dei cursori orizzontali e verticali per fare misure
• un tasto math che permette di visualizzare una combinazione matematica dei segnali presenti agli ingressi

ma le funzioni a disposizione sono molte di più (collegamento diretto con una stampante, memorizzazione via USB, ecc.).

Imparare ad usare un'oscilloscopio non è facile ma è necessario perché è uno dei pochi strumenti veramente fondamentali di un laboratorio di elettronica.

Un segnale periodico può essere sempre scomposto in:

• una componente sinusoidale (non sempre presente)
• la somma di tante sinusoidi dette armoniche, con ampiezza e fase diverse e frequenza multipla di quella del segnale

Vedi anche questa pagina interattiva dove è possibile vedere come un'onda quadra si possa ottenere sommando tante sinusoidi.

• simulazione di figura 28 onda quadra di frequenza variabile e filtro RC
• non solo teoria 2: accordatore con generatore di funzione, resistenza, condensatore e diffusore

Nelle misure indirette (il valore misurato si ottiene con una formula dove compaiono misure dirette di altre grandezze, ad esempio area = base x altezza) gli errori si calcolano così:

• somma e sottrazione (da evitare!): si sommano gli errori assoluti
• prodotto e divisione: si sommano gli errori relativi

Torna all'indice.