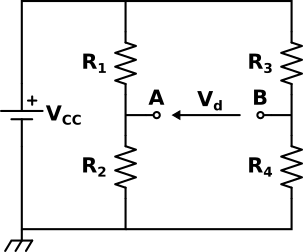
Quattro resistenze collegate in serie a due a due (due rami in parallelo con due resistenze in serie ognuno). Si misura la tensione tra i punti intermedi dei due rami.

Il ponte si usa:

• all'equilibrio, cioè quando la tensione vale zero
• squilibrato, con tensioni diverse da zero

Si usa per misurare una resistenza incognita conoscendo il valore delle altre tre. In genere si procede così:

• due resistenze hanno valore fisso (ad esempio R₃ e R₄) mentre la terza è variabile (R₂)
• si agisce sulla resistenza variabile in modo da azzerare la tensione V_d
• la resistenza incognita (R₁) si calcola con la relazione R₁/R₂=R₃/R₄

Più in generale se V_d è nulla vale:

`V_A=(R_2)/(R_1+R_2) V_(\C\C)`

`V_B=(R_4)/(R_3+R_4) V_(\C\C)`

e uguagliando le due tensioni si ottiene:

`(R_2)/(R_1+R_2)=(R_4)/(R_3+R_4)⇒ R_2(R_3+R_4)=R_4(R_1+R_2) ⇒ R_2 R_3 + R_2 R_4 = R_1 R_4 + R_2 R_4 ⇒ R_1/R_2=R_3/R_4`

Si parte da una condizione di equilibrio con V_d = 0, ad esempio ponendo tutte le resistenze uguali. Se una di queste cambia la tensione V_d non è più nulla ed il suo valore dipende da quanto è cambiata la resistenza. Questa soluzione si usa per i sensori resistivi perché:

• si ottiene una tensione
• la tensione dipende da ΔR e non da R
• la sensibilità è elevata (tensione in uscita anche a fronte di piccole ΔR)
• si possono usare più sensori resistivi contemporaneamente (maggiore sensibilità, minore dipendenza dalla temperatura)

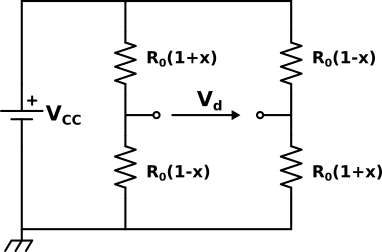
Se, come avviene per le celle di carico, le quattro resistenze sono quattro estensimetri collegati in modo da deformarsi in direzioni opposte a due a due si ottiene il circuito seguente:

Dove R₀ è la resistenze dell'estensimetro a riposo (non deformato) e x=ΔR/R₀ è la variazione relativa della resistenza.

La tensione V_d si calcola così:

`V_d=V_(\C\C) ( (R_0(1+x) )/(R_0(1+x)+R_0(1-x) )-(R_0(1-x) )/(R_0(1+x)+R_0(1-x) ) )=` `=V_(\C\C) (2R_0 x)/(2R_0)=V_(\C\C) cdot x`

Questa configurazione è la migliore possibile perché:

• la relazione tra tensione e ΔR è lineare
• la sensibilità è massima
• la temperatura non influisce sulla misura (tutti gli estensimetri ne sono affetti e cambia solo R₀)

L'unico difetto è che la tensione in uscita non è riferita a massa e richiede un amplificatore differenziale per per poter essere amplificata (meglio ancora un amplificatore per strumentazione).

Un amplificatore per strumentazione è un integrato che permette di amplificare un segnale differenziale (non riferito a massa). E' una soluzione migliore di quella con amplificatore differenziale con operazionale perché:

• presenta una resistenza di ingresso infinita, quindi non carica il sensore che genera il segnale differenziale¹⁾
• è più facile da utilizzare perché il guadagno dipende da un solo resistore/trimmer
• ha in generale prestazioni e precisione migliori

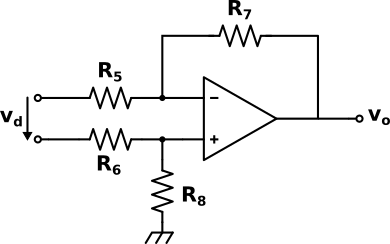
L'integrato contiene tre operazionali, due usati come buffer e uno come stadio differenziale, collegati come nella figura seguente:

La tensione differenziale applicata tra Vin+ e Vin- viene riportata ai capi del resistore R₃(Rg nei datasheet) che fissa il valore della corrente che scorre sulle tre resistenze²⁾; la tensione ai capi delle tre resistenze viene poi riferita a massa dallo stadio amplificatore differenziale di guadagno unitario, realizzato col terzo operazionale e le quattro resistenze uguali. Questo circuito permette di fissare il guadagno tramite la sola Rg - che è esterna all'integrato - e presenta una resistenza di ingresso infinita. Se la Rg non viene collegata il guadagno è uno.

L'amplificatore per strumentazione che abbiamo usato in laboratorio è l'INA111. Non è un componente economico ma ha una buona precisione ed è disponibile nel package DIP, quindi può essere utilizzato anche su breadboard. Il suo datasheet mostra uno schema circuitale interno simile a quello della figura sopra; il guadagno si calcola con la formula:

`A_v = 1+(50k Omega)/R_G`

Esercizio preso da qui.

NB: la configurazione del ponte di Wheatsone proposta nel file PDF, pur funzionando dal punto di vista teorico, non è utilizzabile in pratica. Ponendo la Pt100 nella parte alta del ponte le tensioni ai due estremi della diagonale (V_A e V_B) sono troppo vicine alla tensione di alimentazione dell'operazionale col risultato che l'uscita di quest'ultimo satura e il circuito non funziona. Meglio allora mettere la Pt100 nella parte bassa del ponte.

Progettare un circuito di condizionamento con ponte di Wheatstone e termoresistenza Pt100 (α = 3.85×10^-3 1/°C) tale da avere 0V a 0°C e 10V a 150°C.

Considerato il range di tensione in uscita si sceglie un'alimentazione con Vcc = 12V. Per l'amplificatore operazione serve anche una -Vcc = -12V.

Con uno schema come quello della figura a inizio pagina si sceglie di porre la Pt100 al posto di R1. La tensione in uscita sarà la V_BA, orientata verso destra, perché la tensione tra A e massa cala all'aumentare della temperatura (la resistenza della Pt100 aumenta mentre la R₂ resta costante) mentre la tensione tra B e massa è costante.

La tensione in uscita è differenziale (o flottante) perché nessuno dei due punti è riferito a massa; servirà uno stadio differenziale ad operazionale per riferire la tensione a massa ed amplificarla.

Per limitare l'autoconsumo della Pt100 si impone³⁾ una corrente massima di 2mA. Nelle caso peggiore possibile, considerato il range di temperature indicato nelle specifiche, la resistenza della Pt100 è di 100 Ω. Allora si può scrivere:

`I_max = Vcc/(R_Pt100 + R_2)`

quindi

`R_2 = Vcc/I_max - 100= 5,9 kOmega`

e si sceglie per R₂ il valore commerciale 5,6 kΩ.

Dalle specifiche risulta che a 0°C la tensione in uscita debba valere 0 Volt. Questo avviene quando la tensione differenziale del ponte è nulla, cioè quando il ponte è in equilibrio e vale R1/R2 = R3/R4. Se al posto di R1 mettiamo il valore della resistenza della Pt100 a 0°C (100 Ω) si ottiene la relazione:

`100/5600=R_3/R_4`

Conviene allora porre R₃ = 100 Ω e R₄ = 5,6 kΩ per imporre l'equilibrio del ponte a 0°C.

A 150°C la resistenza della Pt100 vale:

`R_{Pt100} = 100*(1+ alpha T)= 100*(1+3,85×10^(-3)*150)=157.75 Omega`

mentre la tensione nel punto A si vale:

`V_A = (R_2 V_{C\C})/(R_(Pt100) + R_2)=(5,6 cdot 10^3 cdot 12)/(157,75+5600) =11,671 V`

La tensione nel punto B non dipende dalla temperatura e vale sempre:

`V_B = (R_4 V_{C\C})/(R_3 + R_4) = (5,6 cdot 10^3 cdot 12)/(100+ 5,6 cdot 10^3)= 11,789 V`

A 150°C la tensione differenziale del ponte vale allora:

`V_d = V_(BA) = V_B - V_A = 11,789-11,671 ~= 118 mV`

Per ottenere 10 Volt in uscita riferiti a massa è necessario amplificare questo valore. Il guadagno richiesto è:

`A_v = V_{O}/V_d = 10/118 cdot 10^(-3)= 84,4`

Questo valore serve a dimensionare le quattro resistenze dello stadio amplificatore differenziale ad operazionale posto a valle del ponte Wheatstone.

Le quattro resistenze, uguali a due a due per semplicità, fissano il guadagno differenziale:

`v_O = A_d cdot v_d`

con

`A_d= R_8/R_6=R_7/R_5=84,4`

Ponendo R₅ = R₆ = 1 kΩ restano definite R₇ e R₈ come:

`R_7=R_8=84,4 cdot 1 cdot 10^3 = 84,4 k Ohm`

ottenibili con due resistori da 82 kΩ seguiti da due trimmer da 5kΩ.

Torna all'indice.