23D - Trasduttori e condizionamento dei segnali parte seconda

Questa sezione fa parte dei contenuti online (auladigitale) scaricabili da http://www.rcseducation.it e contiene integrazioni alla sezione 23A. Esamineremo solo alcuni argomenti dei paragrafi 2 e 3 per completare l'esame dei circuiti convertitori con operazionali.

Il paragrafo si apre con alcune considerazioni sull'opportunità di utilizzare segnali in corrente quando il trasduttore è lontano dal circuito di acquisizione già esposte nella sezione 23A.

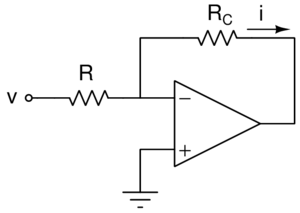
Il metodo più semplice per convertire una tensione in corrente - applicarla ai capi di una resistenza - non è praticabile perché il carico influenza il valore della corrente e la sorgente di segnale è caricata. Una soluzione con operazionale, come quella nella figura seguente, risolve entrambi i problemi ma richiede un carico flottante, cioè con nessuno dei due terminali a massa.

La corrente che percorre il carico è indipendente dal carico stesso e vale:

`i=v/R`

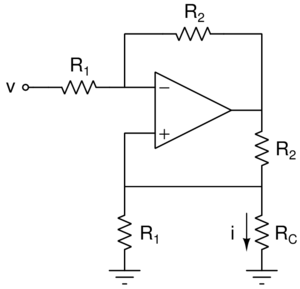
Il circuito seguente permette invece di collegare il carico a massa.

In questa configurazione le corrente che percorre il carico vale:

`i=v/R_1`

La conversione tensione/frequenza (V/f) e frequenza/tensione (f/V) è particolarmente efficace nella trasmissione a distanza di segnali analogici per le sue caratteristiche di immunità ai disturbi e all'attenuazione. Il segnale in frequenza infatti presenta solo due livelli e disturbi ed attenuazione nella trasmissione possono modificano l'ampiezza ma non la frequenza del segnale. Un ulteriore vantaggio di questa tecnica è la facilità con cui è possibile trasformare il segnale in digitale, semplicemente contando gli impulsi del segnale in frequenza.

La figura 21 mostra lo schema di principio di un convertitore tensione/frequenza a bilanciamento di carica (ad esempio l'integrato LM331). Lo schema è piuttosto complesso ¹⁾ e comprende un integratore attivo, un comparatore e un multivibratore monostabile che comanda un generatore di corrente e un buffer invertente. Supponendo il segnale in ingresso costante e negativo e prelvando l'uscita dal buffer il principio di funzionamento è il seguente:

• con l'interruttore SW aperto e v_s negativa l'uscita dell'integratore invertente è una rampa crescente
• quando la tensione v₁ supera V_R il comparatore passa allo stato alto
• il fronte di salita di v₂ fa commutare il monostabile²⁾ e la tensione v₃ resta al livello alto per un tempo t_d costante imposto dai valori di R_t e C_t
• il livello alto di v₃ fa chiudere l'interruttore SW che scarica il condensatore con una corrente costante I ³⁾
• la tensione v₁ ai capi del condensatore fa una rampa decrescente (con pendenza diversa rispetto alla carica)
• dopo il tempo t_d l'interruttore v₃ torna al livello basso e l'interruttore SW si apre
• il ciclo ricomincia con una nuova rampa crescente

La figura 21 aiuta a comprendere il ciclo di funzionamento mostrando l'andamento delle tensioni ai capi del condensatore e in uscita (v₁ e v_o). Come si vede si ha a una fase di scarica di durata costante a corrente costante - quindi a carica Q = I⋅t_d costante - e una di carica di durata variabile con corrente proporzionale alla tensione in ingresso V_s. In altre parole, ogni volta che si attiva il multivibratore una carica costante è sottratta al condensatore; la stessa quantità di carica viene poi ripristinata dall'ingresso ma con un valore di corrente che dipende da V_s e per un tempo variabile. Esprimendo analitacamente il bilancio tra le due cariche vale:

`-V_S/R(t_a + t_d)=-V_s/R cdot T = I cdot t_d`

dove la corrente dall'ingresso scorre sia durante la carica che la scarica e la somma dei due tempi è il periodo T. Allora:

`f= |V_s|/(R cdot I cdot t_d)`

Lo stesso circuito utilizzato per la conversione V/f può essere utilizzato per la conversione frequenza/tensione (f/V) ma con i componenti collegati in maniera leggermente diversa, come mostrato in figura 24. Il segnale in ingresso è applicato al comparatore e l'uscita è prelevata dall'integratore. Il principio di funzionamento è il seguente:

• il segnale v_s in ingresso viene squadrato dal comparatore
• un fronte di salita in uscita al comparatore attiva il monostabile portandolo al livello alto per un tempo t_d costante fissato da R_t e C_t
• il livello alto del monostabile fa chiudere l'interruttore SW che collega il generatore di corrente costante all'integratore
• all'ingresso dell'integratore è presente un treno di impulsi in corrente con:
  • ampiezza costante I
  • durata costante t_d
  • frequenza pari a quella di v_s

In questo circuito l'integratore è usato come filtro passa basso ⁴⁾ per prelevare il valore medio della corrente in ingresso. Osservando l'andamento della corrente di figura 24 si vede che il valore medio è:

`I_m=I t_d/T= I cdot t_d cdot f`

Allora, considerando che l'ingresso invertente dell'integratore è una massa virtuale, vale:

`V_(om)= -I_mR=-I t_d R cdot f`

Quindi la tensione è proporzionale alla frequenza f.

Torna all'indice.