16B - Comparatori e circuiti logaritmici

Vedremo solo i circuiti comparatori.

Un comparatore confronta due segnali e indica qual è il più grande con un valore alto o basso di tensione in uscita.

La soluzione circuitale più semplice per realizzare un comparatore è quella di utilizzare un amplificatore operazionale in catena aperta¹⁾. In questo caso l'operazionale si comporta da amplificatore differenziale con guadagno infinito:

`v_o=A_v(v_+ - v_-) quad , quad A_v=oo `

e satura non appena le due tensioni, invertente e non invertente, sono diverse tra loro:

• se v₊ > v_- la tensione in uscita vale +V_cc²⁾
• se v₊ < v_- la tensione in uscita vale -V_cc

La figura 1a mostra un comparatore non invertente che confronta una tensione in ingresso v_i con una di riferimento V_ref. La corrispondente caratteristica di trasferimento è rappresentata in figura 1b; come si vede l'uscita assume solo due valori a seconda che v_i sia maggiore o minore di V_ref. Scambiando i due ingressi si realizza un comparatore invertente (vedi figura 1c e figura 1d).

Se necessario è possibile adattare la tensione in uscita del comparatore ponendo un limitatore a diodi zener³⁾ in cascata. La figura 2 mostra tre casi con limitatore a un livello (superiore o inferiore) e a due livelli.

Il comparatore a finestra di figura 3a presenta due tensioni di riferimento, V_1ref e V_2ref, e permette di stabilire se la tensione v_i è compresa o meno tra le due di riferimento. Il funzionamento, evidenziato dalla caratteristica di trasferimento di figura 3b, è molto semplice:

• se V_2ref < v_i < V_1ref, le uscite di entrambi gli operazionali valgono -V_CC, i diodi sono interdetti e la tensione in uscita vale zero
• negli altri casi uno dei due operazionali presenta in uscita V_CC, il corrispondente diodo conduce e v_o assume il valore alto di tensione V_oH

• esempio 1: circuito di comando di un elemento riscaldante (complicato ma spunto per rivedere BJT, ponte Wheatstone, diodi zener e introdurre le sonde di temperatura NTC)
• scheda integrativa 16B.1 - i comparatori commerciali (LM311)
• simulare e montare un comparatore a finestra con LM339
• esercizi: 1 (comparatore a finestra), 2 (comparatore con OP-AMP e BJT), 3 (segnale TT da onda triangolare)

I difetti principali dei comparatori sono:

• lentezza in commutazione⁴⁾
• comportamento non corretto in presenza di piccole variazioni del segnale intorno al valore di riferimento (vedi figura 6, dove un disturbo sovrapposto al segnale produce commutazioni indesiderate)

Il comparatore ad isteresi - o trigger di Schmitt - risolve entrabi i problemi:

• la commutazione è veloce per effetto della retroazione positiva
• la commutazione avviene solo oltre una certa soglia per effetto dell'isteresi

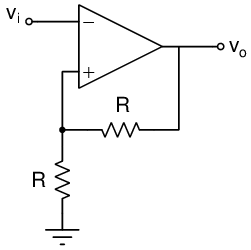
Lo schema seguente mostra l'esempio più semplice di comparatore con isteresi invertente.

Osserviamo che:

• il circuito presenta una retroazione positiva che rende la commutazione più veloce (il guadagno, già elevato ad anello aperto, diventa praticamente infinito)
• quando l'uscita vale +V_CC all'ingresso non invertente è presente una tensione di soglia V_T+ pari a +V_CC/2
• quando l'uscita vale -V_CC all'ingresso non invertente è presente una tensione di soglia V_T- pari a -V_CC/2
• il comportamento è invertente
• in questa configurazione la tensione di riferimento è 0 Volt

In definitiva abbiamo due soglie diverse per la commutazione:

• quando la tensione supera V_T+ l'uscita commuta al livello basso di tensione V_oL
• quando la tensione scende sotto V_T- l'uscita commuta al livello alto di tensione V_oH

come illustrato dalla caratteristica di trasferimento simmetrica di figura 7c.

L'isteresi, cioè la differenza tra V_T+ e V_T-, serve a impedire commutazioni indesiderate nell'intorno della tensione di riferimento.

E' possibile stabilire un valore diverso da ±V_CC/2 per V_T+ e V_T-, basta scegliere opportunamente i valori delle due resistenze. Se indichiamo con R₁ la resistenza sul ramo di retroazione e con R₂ l'altra vale:

`V_T+ = R_2/(R_1 + R_2) V_(\C\C) quad , quad V_T- = -R_2/(R_1 + R_2) V_(\C\C) `

Il circuito di figura 7a mostra il caso più generale del comparatore con isteresi invertente dove la tensione V_ref è diversa zero. In questo caso le due tensioni di soglia si calcolano con⁵⁾:

`V_T+ = R_1/(R_1 + R_2) V_(ref) + R_2/(R_1 + R_2) V_(oH) quad , quad V_T- = R_1/(R_1 + R_2) V_(ref) + R_2/(R_1 + R_2) V_(oL)`

Dove V_oL è minore di zero e i valori delle due tensioni in uscita sono diminuiti di 1÷2 Volt rispetto a V_CC. La caratteristica corrispondente è quella di figura 7b e il comportamento in presenza di disturbi è quello corretto mostrato in figura 8. L'isteresi è la stessa rispetto al caso senza V_ref mentre la tensione di riferimento, cioè il termine costante nelle due tensioni di soglia, è pari a `R_1/(R_1 + R_2) V_(ref)`.

Ragionando in maniera analoga è possibile interpretare il circuito del comparatore con isteresi non ivertente di figura 9. In questo caso si ha la commutazione dal livello basso a quello alto superando V_T+ mentre avviene il contrario scendendo sotto V_T-. I valori delle due soglie si calcolano con:

`V_T+ = (R_1 + R_2)/R_1 V_(ref) - R_2/R_1 V_(oL) quad , quad V_T- = (R_1 + R_2)/R_1 V_(ref) - R_2/R_1 V_(oH) `

• qualcosa al posto di 16B.2 e 16B.3 sui comparatori con e senza isteresi
• esercizi: 4 (dimesionamento trigger di Schmitt)

Torna all'indice.