Indice
Circuito che somma due numeri binari
Con le funzioni logiche è possibile realizzare anche circuiti aritmetici. In questo caso vogliamo realizzare un circuito con porte logiche che calcoli la somma di due numeri binari a due bit.
Semisommatore o half-adder
Se consideriamo la somma di due numeri binari da un bit osserviamo che:
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 con riporto di 1
Se chiamiamo i due addendi A e B, la somma S e il riporto R possiamo riassumere il calcolo in questa tabella:
| A | B | S | R |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
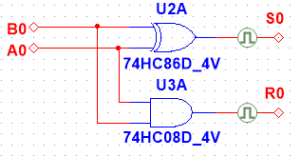
Come si vede la colonna che rappresenta la somma corrisponde a quella della funzione logica EX-OR mentre quella del riporto alla funzione logica AND. Allora è possibile creare un circuito con porte logiche che realizzi la somma aritmetica tra due bit come in figura.
Questo circuito è detto semisommatore.
Sommatore completo o full-adder
Il circuito semisommatore ha dei limiti evidenti, permette di sommare due soli bit e non dispone di un ingresso per sommare l'eventuale riporto di un calcolo precedente. Infatti se consideriamo la somma dei numeri binari 11 (2) e 11(2):
11 11+ 11= ---- 110
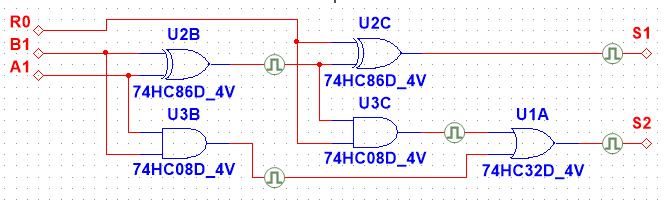
notiamo come, per ogni colonna dell'operazione, non sia sufficiente poter sommare due bit; è necessario poter sommare un terzo addendo, il riporto. Il circuito che permette di sommare due bit e un eventuale riporto è detto sommatore (o full-adder) ed questo:
Il circuito contiene due semisommatori; il primo somma i due bit mentre il secondo somma il risultato con un eventuale riporto per ottenere il risultato vero e proprio. In uscita è presente un riporto se una delle due somme produce un riporto (porta OR)1).
Circuito completo
Con il semisommatore è possibile sommare numeri binari con un numero qualunque di bit, basta disporre i sommatori in cascata con il riporto della somma tra i bit meno significativi in ingresso al sommatore successivo. Nel nostro caso vogliamo sommare due numeri di soli due bit quindi è sufficiente:
- un semisommatore per la somma dei bit meno significativi, dove non c'è mai un riporto di un operazione precedente
- un sommatore per il bit successivo
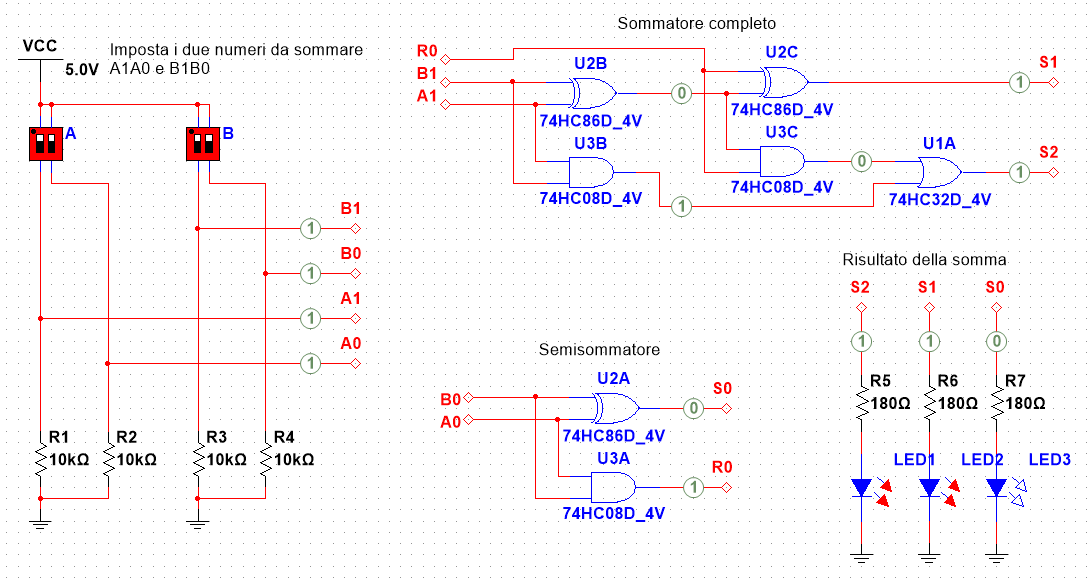
Il circuito completo è il seguente:
Osserviamo che:
- la terza cifra binaria del risultato (il risultato più grande possibile è 6 e servono tre bit) coincide col riporto del sommatore
- i bit dei due numeri sono impostati con degli interruttori dip-switch e resistenze di pull-down
- si ha un'indicazione visiva del risultato con l'accensione dei LED